En esta lección vamos a conocer cuáles son las Operaciones con polinomios, este contenido corresponde al bloque 4 de Matemáticas del primer semestre y a la unidad 2 de la materia de Representaciones simbólicas y algoritmos.
¿Qué es un polinomio?
Un polinomio es una expresión algebraica constituida por un número finito de términos algebraicos; como has visto, cada uno ellos está compuesto por números y letras relacionadas mediante productos y potencias con números naturales.
Ejemplos:

Existen diversos tipos de polinomios: monomios, binomios, trinomios, etcétera. Un monomio es un polinomio que consta de un solo término, por ejemplo: 5x4 y.
Un binomio es el que consta de dos términos, por ejemplo: 7a – 3b3 .
Un trinomio consta de tres términos, por ejemplo: a4 – 3x2 + 8.
El resto de los polinomios se caracterizan por el número de términos que lo componen; así existen polinomios de cuatro términos, de cinco términos, etcétera. Con los polinomios se pueden realizar las mismas operaciones que con los números reales: suma, resta, multiplicación y división.
Suma de polinomios
Para sumar dos o más polinomios simplemente se unen con un signo + y se reducen los términos semejantes. También suelen colocarse uno debajo del otro, de modo que los términos semejantes queden en columna, para facilitar la reducción de éstos. Ejemplos:
Si queremos sumar los polinomios 5x – 4y + 3 y 7x + 2y – 9,
entonces 5x – 4y + 3 + 7x + 2y – 9 = 12x – 2y – 6.
Si queremos sumar los polinomios a2 b – 6b + 3a2 , 4a2 + 2b2 y 7a2 b – 3b – 5b2 – 10, entonces;
a2 b – 6b + 3a2 + 4a2 + 2b2 + 7a2 b – 3b – 5b2 – 10 = 8a2 b – 9b + 7a2 – 3b2 – 10
Si queremos realizar una suma en columna:

Resta de polinomios
Para restar dos o más polinomios restamos del minuendo cada uno de los términos del sustraendo. Para hacerlo, primero debemos anotar el minuendo y, a continuación escribiremos el sustraendo cambiándole el signo a todos sus términos; después reducimos términos semejantes. También pueden colocarse uno debajo del otro, para que los términos semejantes queden en columna, igual que en la suma, pues una vez cambiados los signos del sustraendo lo que se efectúa es una suma.
Ejemplos:
Si queremos restarle al polinomio –8a + 6b + c el polinomio 5a + 2b – 4c, entonces –8a + 6b + c – 5a – 2b + 4c = –13a + 4b + 5c.
Si queremos restarle a 12xy3 – 8x2 + x3 y el polinomio 6x2 – 2x3 y – 4y2 ,
entonces 12xy3 – 8x2 + x3 y – 6x2 + 2x3 y + 4y2 = 12x3 y – 14x2 + 3×3 y + 4y2 .
Si queremos restar un polinomio en columna:
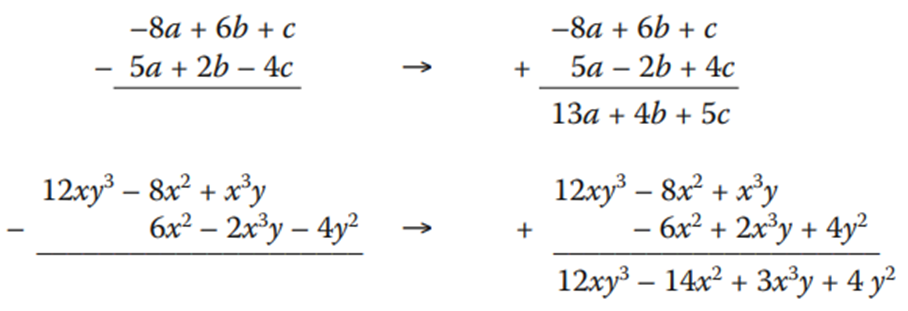
Multiplicación de polinomios
En la multiplicación de polinomios podemos encontrar diversas situaciones que requieren manejarse de manera diferente:
a) Multiplicación de monomios:
Para multiplicar dos o más monomios se multiplican los coeficientes numéricos y las literales aplicando las reglas de los signos y las leyes de los exponentes. Ejemplos:

¡Atención! También podemos utilizar los paréntesis, en lugar del símbolo ∙ o del signo × para indicar la multiplicación, como se constata en los siguientes ejemplos

b) Multiplicación de un monomio por un polinomio
Para multiplicar un monomio por un polinomio aplicamos la propiedad distributiva. ¿La recuerdas? Es aquella que indica que el producto de un número por la suma de otros dos, es igual a la suma de los productos de cada uno de los sumandos por ese número, es decir, a(b + c) = ab + ac. Ejemplo:
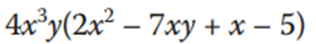
Para multiplicar el monomio 4x3 y por el polinomio 2x2 – 7xy + x – 5, aplico la propiedad distributiva y multiplico 4×3 y por cada uno de los términos del polinomio.
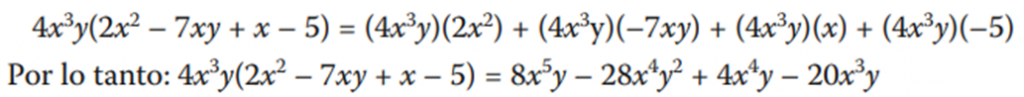
c) Multiplicación de dos polinomios
Para multiplicar dos polinomios debemos multiplicar cada término del primer polinomio por todos los términos del segundo y sumarlos o restarlos dependiendo de la operación que enlace los términos del primer polinomio. Si estudias los siguientes ejemplos, podrás observar los pasos que debemos realizar:
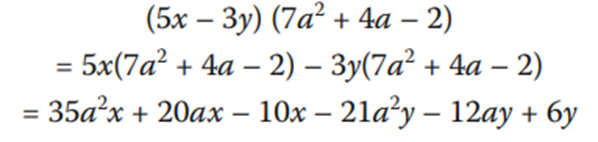
Nota cómo en el segundo paso hemos convertido la multiplicación de polinomios en una resta de dos multiplicaciones de monomio con polinomio, que ya podemos resolver con el procedimiento que estudiaste en el inciso anterior. Estudia este otro ejemplo:
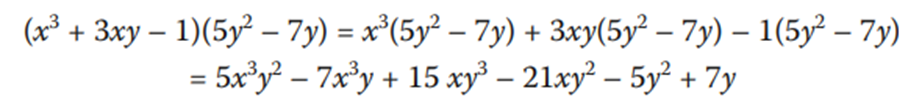
Observa cómo lo que hacemos es convertir la multiplicación de polinomios en una suma o resta de multiplicaciones de monomio con polinomio, operación que aprendimos a manejar en el inciso anterior.
División de polinomios
La división de polinomios también se presenta en diversas formas:
a) División de un monomio entre un monomio
Para dividir un monomio entre otro, se dividen los coeficientes numéricos y se aplican las leyes de los exponentes. Ejemplos:

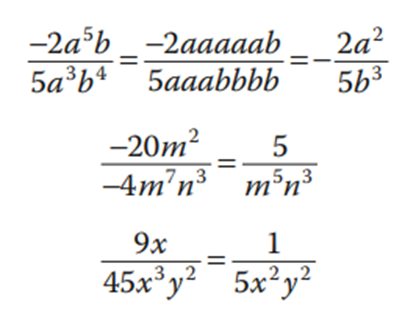
b) División de un polinomio entre un monomio
Para dividir un polinomio entre un monomio se aplica la propiedad distributiva y se divide cada término entre el monomio. Ejemplos:
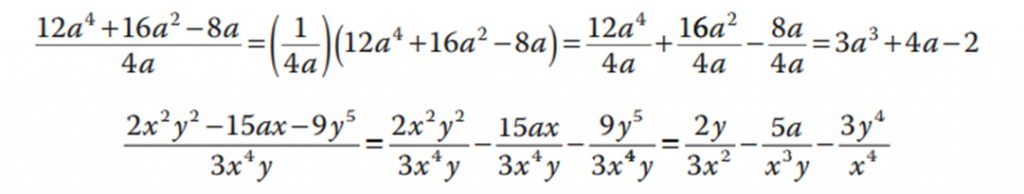

Excelente apoyo, muchas gracias