En esta lección vamos a conocer las propiedades de igualdad y como aplicarlas en las ecuaciones, este contenido corresponde al bloque 1 de Matemáticas del primer semestre y a la unidad 1 de la materia de Representaciones simbólicas y algoritmos.
¿Qué son las propiedades de igualdad?
Con el fin de encontrar los valores de las incógnitas en una ecuación, es necesario ir transformando la ecuación hasta que la incógnita quede de un lado y los números que se conocen del otro, pero sin alterar la igualdad.
De esta manera una vez realizadas las operaciones matemáticas implicadas sabremos el valor de la incógnita. Para hacer esas transformaciones se deben usar las propiedades de la igualdad, que se enuncian a continuación.
Propiedades de igualdad de la suma
Si a, b y c son números reales cualesquiera tales que a = b, entonces a + c = b + c. En otras palabras, puedo sumar el mismo número a los dos lados de la igualdad y seguirá siendo una igualdad.
Ejemplo:
3 + 2 = 4 + 1. Ambos lados de la ecuación son iguales a 5. Si sumo 7 de los dos lados, ahora ambos serán iguales a 12. 3 + 2 + 7 = 4 + 1 + 7
Sumar una cantidad de ambos lados de la ecuación nos permite pasar números de un lado a otro a partir de sumar los inversos aditivos de un número.
Por ejemplo, si tenemos x + 4 = 15, entonces sumamos – 4 de ambos lados de la ecuación y lo que sucederá es que del lado izquierdo se eliminará el 4, y del lado derecho aparecerá un – 4, pero éste lo podemos sumar con el 15. Es decir que el 4 pasará del otro lado de la igualdad con el signo inverso.
x + 4 – 4 = 15 – 4. Como + 4 – 4 = 0, del lado derecho solo queda la x y la ecuación ahora es x = 15 – 4, si los términos del lado derecho se restan nos queda entonces x = 11
Propiedad de la multiplicación
Si a, b y c son números reales cualesquiera tales que a = b, entonces a × c = b × c, es decir, puedo multiplicar los dos lados de la igualdad por el mismo número sin afectar la igualdad.
Ejemplo:
3 + 2 = 4 + 1, ambos lados de la ecuación son iguales a 5. Si multiplico por 2 a los dos lados, ahora ambos serán iguales a 10.
(3 + 2) × 2 = (4 + 1) × 2
Multiplicar una cantidad de ambos lados de la ecuación nos será útil para dejar sola a la incógnita cuando se encuentra dividida por un número. Si multiplicamos por el inverso multiplicativo de este número, nos dará 1, y entonces x × 1 = x.
Por ejemplo, si tenemos la ecuación: x/5 = 6, y multiplicamos por 5 a ambos lados de la igualdad, 5X x/5 = 5 × 6, entonces del lado izquierdo estoy multiplicando por 5 y dividiendo entre 5, y eso es igual a 1. Por lo tanto solo nos queda x, y del lado derecho podemos multiplicar los números que ahí se encuentran, quedando la ecuación x = 6 × 5 = 30
Propiedad de la división
Si a, b y c son números reales cualesquiera tales que a = b, y c ≠ 0, entonces
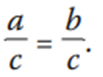
Ejemplo: 3 + 2 = 4 + 1, ambos lados de la ecuación son iguales a 5. Si divido por 2 de los dos lados,
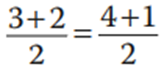
ahora ambos son iguales a 2.5.
Dividir una cantidad de ambos lados de la ecuación nos ayudará para dejar sola a la incógnita cuando se encuentra multiplicada por un número. Si dividimos por el inverso multiplicativo de este número, obtendremos 1 y de nuevo tenemos que x × 1 = x.
Por ejemplo, si tenemos la ecuación: 7 x = 35 y dividimos entre 7 de ambos lados de la ecuación, tendremos

del lado izquierdo

y queda la x sola, del lado derecho hacemos la división y quedará entonces x = 5.
Propiedad de la potencia
Si a, y b son números reales cualesquiera tales que a = b, entonces an = bn .
Ejemplo:
3 + 2 = 4 + 1, ambos lados de la ecuación son iguales a 5. Si elevo al cuadrado de los dos lados, ahora ambos son iguales a 25, (3 + 2)2 = (4 + 1)2
Esta propiedad es útil cuando encontramos raíces en las ecuaciones. Por ejemplo:
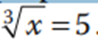
Elevar al cubo a ambos lados de la ecuación nos permite dejar sola a la x pues elevar al cubo y sacar raíz cubica son operaciones inversas y devuelven el mismo número. Por lo tanto:
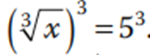
Del lado izquierdo obtenemos x, y del lado derecho realizamos la operación: x = 125
Propiedad de la raíz
Si a, y b son números reales cualesquiera tales que a = b, entonces
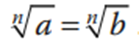
Ejemplo: 3 + 2 = 4 + 1, ambos lados de la ecuación son iguales a 5. Si obtengo la raíz cuadrada de los dos lados
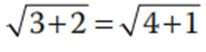
ahora ambos son iguales a 2.236067…
Esta propiedad nos sirve cuando encontramos potencias en las ecuaciones. Por ejemplo: x3 = 512. Utilizando el mismo razonamiento que en la propiedad anterior, de que elevar al cubo y sacar raíz cúbica son operaciones inversas y devuelven el mismo número, ahora corresponde obtener la raíz cúbica de ambos lados de la ecuación. Por lo tanto
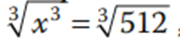
Del lado izquierdo obtenemos x, y del lado derecho realizamos la operación y la ecuación queda x = 8
Como puedes ver en los ejemplos, las propiedades de la igualdad se utilizan para resolver ecuaciones, es decir, para encontrar las incógnitas de éstas. Para lograrlo debemos despejar la x, que significa dejarla sola en uno de los lados de la ecuación. Esto es de gran utilidad para resolver problemas.
